Definitions (of several geometric terms)
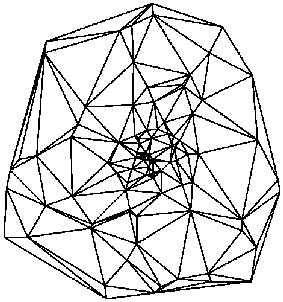
A Delaunay triangulation
of a point set is a triangulation of the point
set with the property that no point in the point set falls in the
interior of the circumcircle (circle that passes through all three
vertices) of any triangle in the triangulation.

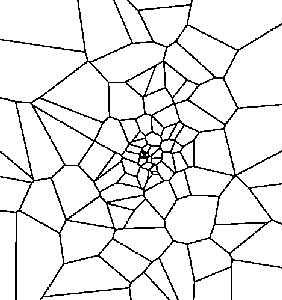
A Voronoï diagram
of a point set is a subdivision of the plane into
polygonal regions (some of which may be infinite), where each region is
the set of points in the plane that are closer to some input point than to
any other input point. (The Voronoï diagram is the geometric dual of the
Delaunay triangulation.)

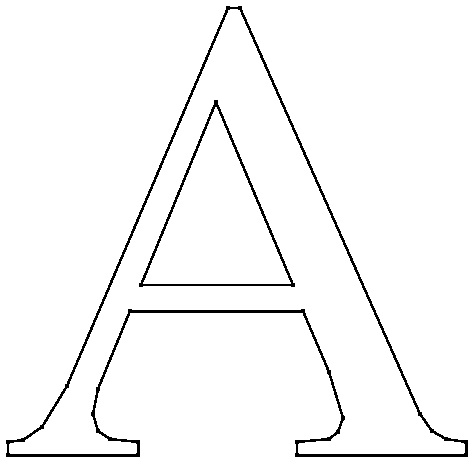
A Planar Straight Line Graph (PSLG)
is a collection of points and segments.
Segments are edges
whose endpoints are points in the PSLG, and whose presence in any
mesh generated from the PSLG is enforced.
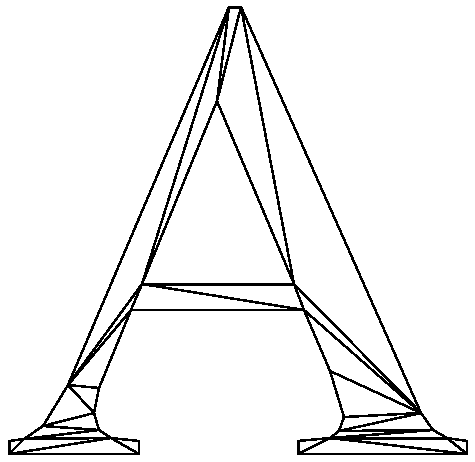
A constrained Delaunay triangulation
of a PSLG is similar to a Delaunay
triangulation, but each PSLG segment is present as a single edge in the
triangulation. (A constrained Delaunay triangulation is not truly a
Delaunay triangulation.)
A conforming Delaunay triangulation
of a PSLG is a true Delaunay
triangulation in which each PSLG segment may have been subdivided into
several edges by the insertion of additional points, called
Steiner points. Steiner
points are necessary to allow the segments to exist in the mesh while
maintaining the Delaunay property. Steiner points are also inserted
to meet constraints on the minimum angle and maximum triangle area.
Return to Triangle home page.
jrs@cs.cmu.edu








